AJohn Blog

外观

Dirichlet-Based Prediction Calibration for Learning with Noisy Labels

约 3012 字大约 10 分钟

2025-03-19

一种基于dirichlet的预测校准(DPC)方法，实现更可靠的模型预测

介绍

带噪声标签的学习严重影响了深度神经网络(dnn)的泛化性能。现有的方法通过损失校正或样本选择方法来解决这个问题。然而，这些方法通常依赖于从softmax函数获得的模型预测，这可能过于自信和不可靠。在这项研究中，我们认为softmax函数的平移不变性是导致这一问题的根本原因，并提出了基于dirichlet的预测校准(DPC)方法作为解决方案。我们的方法引入了一个校准的softmax函数，该函数通过在指数项中加入合适的常数来打破平移不变性，从而实现更可靠的模型预测。为了确保稳定的模型训练，我们利用狄利克雷分布将概率分配给预测的标签，并引入了一种新的证据深度学习(EDL)损失。所提出的损失函数鼓励给定标签的正的和足够大的logits，而惩罚其他标签的负的和小的logits，导致更明显的logits，并促进基于大边际标准的更好的示例选择。通过对不同基准数据集的广泛实验，我们证明DPC达到了最先进的性能。

  • 损失校正：通过估计噪声转移矩阵、调整样本标签或权重来纠正损失

  • 样本选择：根据小损失准则将干净的样本与有噪声的样本分开，其中假设低损失的样本具有干净的标签，并进一步将识别的错误标记的样本视为未标记的样本来进行半监督学习。

但它们中的大多数通常都存在不可靠性问题，因为标准dnn很容易产生过度自信但不正确的预测。

过度置信度现象：

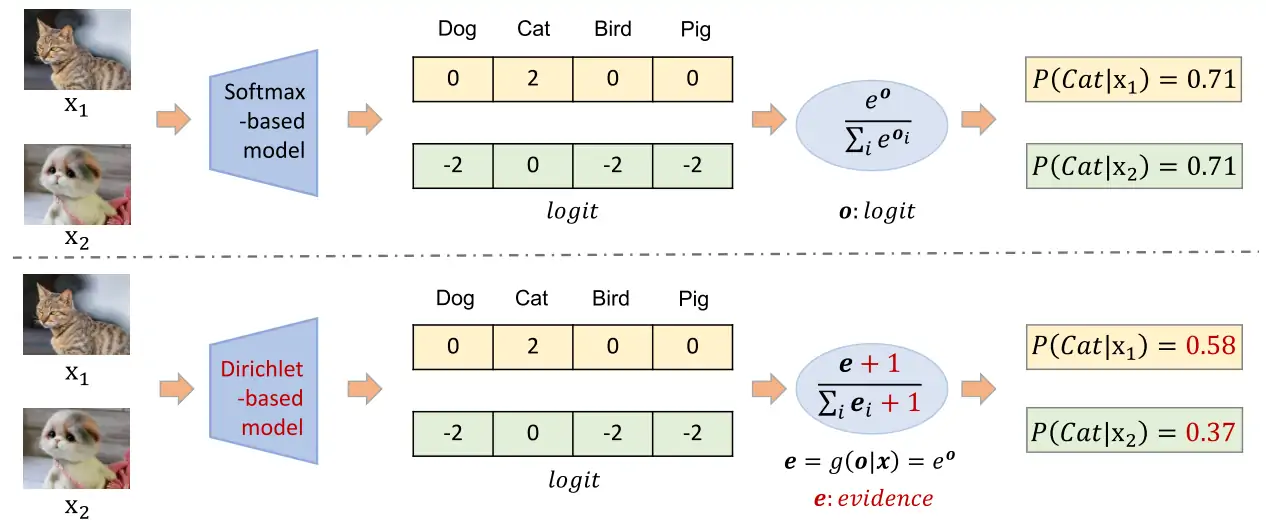
softmax函数的平移不变性：即在所有logits中添加或减去一个常数并不会改变softmax的值;这实际上提高了错误分类的概率——在噪声标签学习中，错误标记的例子被分类为干净的。

Softmax 例子：

Softmax 计算公式如下：

Si=ezi∑jezjS_{i} = \frac{e^{z_{i}}}{\sum_{j} e^{z_{j}}}

其中， z 是输入的 logits，SiS_i 是第 i 个类别的 softmax 概率。

  1. 给定向量 [0, 2, 0, 0]，计算第二个类别（索引为 1）的 softmax 概率：

    S1=e2e0+e2+e0+e0=7.38910.389=0.711S_1 = \frac{e^2}{e^0 + e^2 + e^0 + e^0} = \frac{7.389}{10.389} = 0.711

  2. 给定向量 [-2, 0, -2, -2]，计算第二个类别（索引为 1）的 softmax 概率：

    S1=e0e−2+e0+e−2+e−2=11.4059=0.711S_1 = \frac{e^0}{e^{-2} + e^0 + e^{-2} + e^{-2}} = \frac{1}{1.4059} = 0.711

Softmax 只能反映对数之间的相对关系，并且对x1和x2给出了相同的预测，这与我们的主观直觉相矛盾，因此，引入了 Dirichlet ：

Dirichlet 例子：

Dirichlet 计算公式如下：

Si=ezi+1∑jezj+1S_{i} = \frac{e^{z_{i}} + 1}{\sum_{j} e^{z_{j}} + 1}

其中， z 是输入的 logits，SiS_i 是第 i 个类别的 Dirichlet 概率。

  1. 给定向量 [0, 2, 0, 0]，计算第二个类别（索引为 1）的 Dirichlet 概率：

    S1=e2+1e0+e2+e0+e0+4=8.38914.389=0.583S_1 = \frac{e^2 + 1}{e^0 + e^2 + e^0 + e^0 + 4} = \frac{8.389}{14.389} = 0.583

  2. 给定向量 [-2, 0, -2, -2]，计算第二个类别（索引为 1）的 Dirichlet 概率：

    S1=e0+1e−2+e0+e−2+e−2+4=25.4059=0.370S_1 = \frac{e^0 + 1}{e^{-2} + e^0 + e^{-2} + e^{-2} + 4} = \frac{2}{5.4059} = 0.370

Q1：为什么两个不同的输入得到相同的概率？

Softmax 具有 平移不变性，即如果对所有 logits 加上同一个常数 c，由于指数的性质 ex+c=ex×ece^{x+c} = e^x \times e^c ， 分子分母同时除以 ece^c ，最终 Softmax 结果不会改变。

Q2：+1 的目的？

第一点

在softmax函数的指数项上放置一个合适的常数，可以很容易地打破 Softmax 的平移不变性，并校准模型预测。

第二点

选择 +1 可以让整体预测更加保守，

(a)显示了DivideMix对CIFAR-10测试数据在50%对称噪声下的ECE结果，ECE值越小越好，相应的，更接近虚线的线是优选的。

(b) DivideMix 过于自信的模型预测

我们可以看到，基于 Softmax 的 DivideMix 倾向于产生过于自信的预测，即模型变得过于自信，产生不可靠的预测概率。

想法：将指数移动平均引入标签修复过程，以缓解瞬时预测引起的不稳定问题

Q3：Dirichlet-Based model 相对于 Softmax-Based model 的优势？

无论是样本选择还是标签修复，都高度依赖于模型预测的质量，如果预测的概率更接近真实概率，那么模型就可以更精确地选择干净的样本。

Softmax-Based model：softmax函数的平移不变性会导致噪声标签学习中的过度置信度现象，例如，具有x2等logit的潜在错误标记示例可能最终具有与具有x1等logit的干净示例相同的概率，尽管它们的logits明显小于x1。这使得模型很难有效地执行标签校正或样本选择。

二阶段结合半监督

(c)训练样例的给定标签logit的分布。

(d)样本选择标准的比较。我们可以看到，提出的大边际准则可以产生更具判别性的结果。

DPC为logit赋予了更具体的含义，其中logit大于/小于0表示有证据/没有证据表明属于该类的示例。

实验结果：

EDL_Loss 67.90

平滑项+0.01 先验信息×75.1

效果：

>> Epoch: 20 | R1: 86.5202% | R5: 96.0808% | R10: 97.3575% | mAP: 59.5389% (Best Epoch[20]) | Evaluation time: 62.80s
>> Epoch: 50 | R1: 89.9347% | R5: 97.1496% | R10: 97.9513% | mAP: 67.9090% (Best Epoch[50]) | Evaluation time: 63.14s
alpha = torch.exp(logits) + 10. / self.num_classes

new_alpha = one_hot_y + (1.0 - one_hot_y) * (self.num_classes / 10.) * alpha
------------alpha之前是什么---------
tensor([[0.9914, 0.9363, 1.0505,  ..., 0.9961, 1.0434, 0.9965],
        [0.9644, 0.9882, 1.0147,  ..., 0.9941, 1.0127, 1.0448],
        [1.0121, 1.0021, 0.9804,  ..., 1.0184, 1.0056, 1.0186],
        ...,
        [1.0266, 0.9685, 0.9565,  ..., 0.9526, 1.0873, 1.0191],
        [0.9563, 0.9762, 0.9718,  ..., 0.9779, 1.0101, 1.0076],
        [0.9959, 1.0046, 1.0105,  ..., 1.0435, 1.0234, 1.0075]],
       device='cuda:1', grad_fn=<ExpBackward0>)
------------alpha加平滑是什么---------
tensor([[1.0047, 0.9496, 1.0638,  ..., 1.0094, 1.0568, 1.0098],
        [0.9777, 1.0015, 1.0280,  ..., 1.0074, 1.0260, 1.0581],
        [1.0254, 1.0154, 0.9938,  ..., 1.0317, 1.0189, 1.0319],
        ...,
        [1.0399, 0.9819, 0.9698,  ..., 0.9659, 1.1006, 1.0324],
        [0.9696, 0.9895, 0.9851,  ..., 0.9912, 1.0234, 1.0209],
        [1.0092, 1.0179, 1.0238,  ..., 1.0568, 1.0367, 1.0208]],
       device='cuda:1', grad_fn=<AddBackward0>)
------------one_hot_y是什么---------
tensor([[0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        ...,
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.]], device='cuda:1')
------------new_alpha是什么---------
tensor([[75.4512, 71.3126, 79.8941,  ..., 75.8092, 79.3631, 75.8353],
        [73.4235, 75.2122, 77.2013,  ..., 75.6540, 77.0546, 79.4619],
        [77.0082, 76.2564, 74.6312,  ..., 77.4820, 76.5201, 77.4943],
        ...,
        [78.0973, 73.7381, 72.8334,  ..., 72.5391, 82.6534, 77.5341],
        [72.8144, 74.3137, 73.9846,  ..., 74.4367, 76.8610, 76.6681],
        [75.7933, 76.4435, 76.8905,  ..., 79.3675, 77.8586, 76.6630]],
       device='cuda:1', grad_fn=<AddBackward0>)

训练一段时间后：

------------alpha之前是什么---------
tensor([[1.5934e-04, 1.2289e-03, 2.7540e-03,  ..., 2.3317e-03, 5.6642e-04,
         1.1681e-03],
        [7.0628e-06, 1.6308e-04, 6.2606e-04,  ..., 7.8735e-04, 4.0736e-05,
         5.5734e-04],
        [3.2240e-03, 1.9303e-02, 8.5827e-03,  ..., 3.3928e-03, 8.5747e-03,
         5.8558e-02],
        ...,
        [3.3436e-05, 5.8364e-05, 6.4026e-04,  ..., 1.3241e-05, 3.3979e-05,
         1.3851e-03],
        [7.3420e-03, 5.6132e-05, 1.1281e-02,  ..., 7.6524e-05, 2.9025e-03,
         2.9780e-04],
        [5.8269e-04, 4.4427e-05, 3.5368e-04,  ..., 1.2792e-05, 7.2819e-04,
         7.4317e-06]], device='cuda:1', grad_fn=<ExpBackward0>)
------------alpha加平滑是什么---------
tensor([[0.0135, 0.0145, 0.0161,  ..., 0.0156, 0.0139, 0.0145],
        [0.0133, 0.0135, 0.0139,  ..., 0.0141, 0.0134, 0.0139],
        [0.0165, 0.0326, 0.0219,  ..., 0.0167, 0.0219, 0.0719],
        ...,
        [0.0133, 0.0134, 0.0140,  ..., 0.0133, 0.0133, 0.0147],
        [0.0207, 0.0134, 0.0246,  ..., 0.0134, 0.0162, 0.0136],
        [0.0139, 0.0134, 0.0137,  ..., 0.0133, 0.0140, 0.0133]],
       device='cuda:1', grad_fn=<AddBackward0>)
------------one_hot_y是什么---------
tensor([[0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        ...,
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.]], device='cuda:1')
------------new_alpha是什么---------
tensor([[1.0120, 1.0923, 1.2068,  ..., 1.1751, 1.0425, 1.0877],
        [1.0005, 1.0122, 1.0470,  ..., 1.0591, 1.0031, 1.0419],
        [1.2421, 2.4497, 1.6446,  ..., 1.2548, 1.6440, 5.3977],
        ...,
        [1.0025, 1.0044, 1.0481,  ..., 1.0010, 1.0026, 1.1040],
        [1.5514, 1.0042, 1.8472,  ..., 1.0057, 1.2180, 1.0224],
        [1.0438, 1.0033, 1.0266,  ..., 1.0010, 1.0547, 1.0006]],
       device='cuda:1', grad_fn=<AddBackward0>)

EDL_Loss_plus 69.84

平滑项+1 先验信息×7.51

效果：

>> Epoch: 20 | R1: 87.7375% | R5: 96.6449% | R10: 97.8919% | mAP: 60.7998% (Best Epoch[20]) | Evaluation time: 97.19s
>> Epoch: 52 | R1: 90.8551% | R5: 97.2981% | R10: 98.2779% | mAP: 69.8422% (Best Epoch[52]) | Evaluation time: 141.45s
------------alpha之前是什么---------
tensor([[0.9914, 0.9363, 1.0505,  ..., 0.9961, 1.0434, 0.9965],
        [0.9644, 0.9882, 1.0147,  ..., 0.9941, 1.0127, 1.0448],
        [1.0121, 1.0021, 0.9804,  ..., 1.0184, 1.0056, 1.0186],
        ...,
        [1.0266, 0.9685, 0.9565,  ..., 0.9526, 1.0873, 1.0191],
        [0.9563, 0.9762, 0.9718,  ..., 0.9779, 1.0101, 1.0076],
        [0.9959, 1.0046, 1.0105,  ..., 1.0435, 1.0234, 1.0075]],
       device='cuda:0', grad_fn=<ExpBackward0>)
------------alpha加平滑是什么---------
tensor([[1.9914, 1.9363, 2.0505,  ..., 1.9961, 2.0434, 1.9965],
        [1.9644, 1.9882, 2.0147,  ..., 1.9941, 2.0127, 2.0448],
        [2.0121, 2.0021, 1.9804,  ..., 2.0184, 2.0056, 2.0186],
        ...,
        [2.0266, 1.9685, 1.9565,  ..., 1.9526, 2.0873, 2.0191],
        [1.9563, 1.9762, 1.9718,  ..., 1.9779, 2.0101, 2.0076],
        [1.9959, 2.0046, 2.0105,  ..., 2.0435, 2.0234, 2.0075]],
       device='cuda:0', grad_fn=<AddBackward0>)
------------one_hot_y是什么---------
tensor([[0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        ...,
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.]], device='cuda:0')
------------new_alpha是什么---------
tensor([[14.9551, 14.5413, 15.3994,  ..., 14.9909, 15.3463, 14.9935],
        [14.7523, 14.9312, 15.1301,  ..., 14.9754, 15.1155, 15.3562],
        [15.1108, 15.0356, 14.8731,  ..., 15.1582, 15.0620, 15.1594],
        ...,
        [15.2197, 14.7838, 14.6933,  ..., 14.6639, 15.6753, 15.1634],
        [14.6914, 14.8414, 14.8085,  ..., 14.8537, 15.0961, 15.0768],
        [14.9893, 15.0543, 15.0991,  ..., 15.3467, 15.1959, 15.0763]],
       device='cuda:0', grad_fn=<AddBackward0>)
------------alpha之前是什么---------
tensor([[2.1107e-02, 2.7302e-01, 4.6790e-02,  ..., 9.4812e-01, 3.6484e-02,
         2.4908e-02],
        [2.3904e-02, 2.8858e-01, 8.2517e-02,  ..., 2.0345e-02, 3.5677e-01,
         3.3378e-01],
        [6.0339e-02, 5.1470e-02, 2.1549e-01,  ..., 4.9159e-02, 3.2847e-01,
         5.8174e-01],
        ...,
        [1.7546e-03, 9.9967e-03, 2.4322e-01,  ..., 6.3487e-03, 5.5872e-02,
         3.8229e-03],
        [8.7967e-02, 8.8145e-03, 3.6313e-02,  ..., 3.7381e-03, 1.0505e-02,
         4.8430e-03],
        [1.2621e-04, 2.1394e-01, 2.0034e-03,  ..., 4.6110e-04, 6.1999e-03,
         1.2178e-02]], device='cuda:0', grad_fn=<ExpBackward0>)
------------alpha加平滑是什么---------
tensor([[1.0211, 1.2730, 1.0468,  ..., 1.9481, 1.0365, 1.0249],
        [1.0239, 1.2886, 1.0825,  ..., 1.0203, 1.3568, 1.3338],
        [1.0603, 1.0515, 1.2155,  ..., 1.0492, 1.3285, 1.5817],
        ...,
        [1.0018, 1.0100, 1.2432,  ..., 1.0063, 1.0559, 1.0038],
        [1.0880, 1.0088, 1.0363,  ..., 1.0037, 1.0105, 1.0048],
        [1.0001, 1.2139, 1.0020,  ..., 1.0005, 1.0062, 1.0122]],
       device='cuda:0', grad_fn=<AddBackward0>)
------------one_hot_y是什么---------
tensor([[0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        ...,
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.],
        [0., 0., 0.,  ..., 0., 0., 0.]], device='cuda:0')
------------new_alpha是什么---------
tensor([[ 7.6685,  9.5604,  7.8614,  ..., 14.6304,  7.7840,  7.6971],
        [ 7.6895,  9.6772,  8.1297,  ...,  7.6628, 10.1893, 10.0167],
        [ 7.9631,  7.8965,  9.1283,  ...,  7.8792,  9.9768, 11.8788],
        ...,
        [ 7.5232,  7.5851,  9.3366,  ...,  7.5577,  7.9296,  7.5387],
        [ 8.1706,  7.5762,  7.7827,  ...,  7.5381,  7.5889,  7.5464],
        [ 7.5109,  9.1167,  7.5250,  ...,  7.5135,  7.5566,  7.6015]],
       device='cuda:0', grad_fn=<AddBackward0>)

EDL_Loss_plus2 69.95

平滑项+1 先验信息×1

>> Epoch: 20 | R1: 86.6390% | R5: 96.4667% | R10: 97.8622% | mAP: 60.8740% (Best Epoch[20]) | Evaluation time: 65.94s
>> Epoch: 52 | R1: 90.0238% | R5: 97.4466% | R10: 98.6342% | mAP: 69.9596% (Best Epoch[52]) | Evaluation time: 84.54s

最好 EDL_Loss_plus2 70.42

平滑项+1.07 先验信息×1

>> Epoch: 20 | R1: 87.5594% | R5: 95.8432% | R10: 97.1793% | mAP: 61.8537% (Best Epoch[20]) | Evaluation time: 74.55s
>> Epoch: 52 | R1: 90.9442% | R5: 97.2981% | R10: 98.2185% | mAP: 70.4282% (Best Epoch[52]) | Evaluation time: 207.58s

EDL_Loss_plus2 69.11

平滑项+1.5 先验信息×1

>> Epoch: 20 | R1: 86.1936% | R5: 95.5760% | R10: 97.3278% | mAP: 59.7017% (Best Epoch[20]) | Evaluation time: 104.90s
>> Epoch: 54 | R1: 90.0238% | R5: 97.1793% | R10: 98.0404% | mAP: 69.1196% (Best Epoch[54]) | Evaluation time: 124.93s

EDL_Loss_plus2 69.61

平滑项+2 先验信息×1

>> Epoch: 20 | R1: 86.1045% | R5: 95.5760% | R10: 97.3575% | mAP: 60.2009% (Best Epoch[20]) | Evaluation time: 104.30s
>> Epoch: 54 | R1: 90.1128% | R5: 96.9715% | R10: 98.2779% | mAP: 69.6103% (Best Epoch[54]) | Evaluation time: 192.07s

EDL_Loss_plus2_va 调参

delta 0.1

>> Epoch: 20 | R1: 87.8860% | R5: 96.1105% | R10: 97.4762% | mAP: 61.5247% (Best Epoch[20]) | Evaluation time: 60.89s
>> Epoch: 54 | R1: 90.8848% | R5: 97.1496% | R10: 98.1591% | mAP: 70.2351% (Best Epoch[54]) | Evaluation time: 61.39s

delta 0.5

>> Epoch: 20 | R1: 87.2922% | R5: 96.1698% | R10: 97.5653% | mAP: 61.5106% (Best Epoch[20]) | Evaluation time: 61.80s
>> Epoch: 38 | R1: 90.3504% | R5: 97.1200% | R10: 98.0404% | mAP: 69.1605% (Best Epoch[38]) | Evaluation time: 61.33s

delta 2

>> Epoch: 20 | R1: 86.4905% | R5: 95.9323% | R10: 97.4169% | mAP: 61.1193% (Best Epoch[20]) | Evaluation time: 67.34s
>> Epoch: 34 | R1: 90.3504% | R5: 96.7043% | R10: 97.8028% | mAP: 68.6571% (Best Epoch[34]) | Evaluation time: 67.01s

delta 3

>> Epoch: 20 | R1: 86.9656% | R5: 96.4074% | R10: 97.6544% | mAP: 60.8494% (Best Epoch[20]) | Evaluation time: 66.17s
>> Epoch: 56 | R1: 89.7862% | R5: 97.3278% | R10: 98.1591% | mAP: 69.9605% (Best Epoch[56]) | Evaluation time: 63.01s

好：delta 4

>> Epoch: 20 | R1: 87.5297% | R5: 96.6449% | R10: 97.9810% | mAP: 61.9592% (Best Epoch[20]) | Evaluation time: 63.68s
>> Epoch: 48 | R1: 90.4691% | R5: 97.3872% | R10: 98.6639% | mAP: 70.6581% (Best Epoch[48]) | Evaluation time: 62.32s

delta 5

>> Epoch: 20 | R1: 87.3812% | R5: 96.3777% | R10: 97.7435% | mAP: 61.5462% (Best Epoch[20]) | Evaluation time: 62.50s
>> Epoch: 36 | R1: 90.1425% | R5: 97.2684% | R10: 98.1888% | mAP: 69.0767% (Best Epoch[36]) | Evaluation time: 61.86s

正常是 gamma 1

gamma 0.1

>> Epoch: 20 | R1: 87.6781% | R5: 96.5558% | R10: 97.8028% | mAP: 61.8076% (Best Epoch[20]) | Evaluation time: 63.71s
>> Epoch: 52 | R1: 90.0534% | R5: 97.3872% | R10: 98.4264% | mAP: 70.4326% (Best Epoch[52]) | Evaluation time: 61.80s

gamma 0.5

>> Epoch: 20 | R1: 87.2031% | R5: 95.7542% | R10: 97.3872% | mAP: 61.8113% (Best Epoch[20]) | Evaluation time: 66.93s
>> Epoch: 58 | R1: 90.0831% | R5: 97.3278% | R10: 98.3076% | mAP: 70.1560% (Best Epoch[58]) | Evaluation time: 62.94s

gamma 2

>> Epoch: 20 | R1: 87.1437% | R5: 96.3777% | R10: 97.9810% | mAP: 60.4109% (Best Epoch[20]) | Evaluation time: 67.48s
>> Epoch: 40 | R1: 90.2613% | R5: 97.2684% | R10: 98.1591% | mAP: 68.6607% (Best Epoch[40]) | Evaluation time: 65.91s

gamma 5

>> Epoch: 20 | R1: 87.5891% | R5: 96.2292% | R10: 97.5653% | mAP: 61.6208% (Best Epoch[20]) | Evaluation time: 61.47s
>> Epoch: 50 | R1: 90.6473% | R5: 97.2090% | R10: 98.1295% | mAP: 69.9455% (Best Epoch[50]) | Evaluation time: 61.82s

core_dpc_here_plus2_s 调参