一、定长滑动窗口

1.1 基础

定长滑窗套路 我总结成三步：入-更新-出。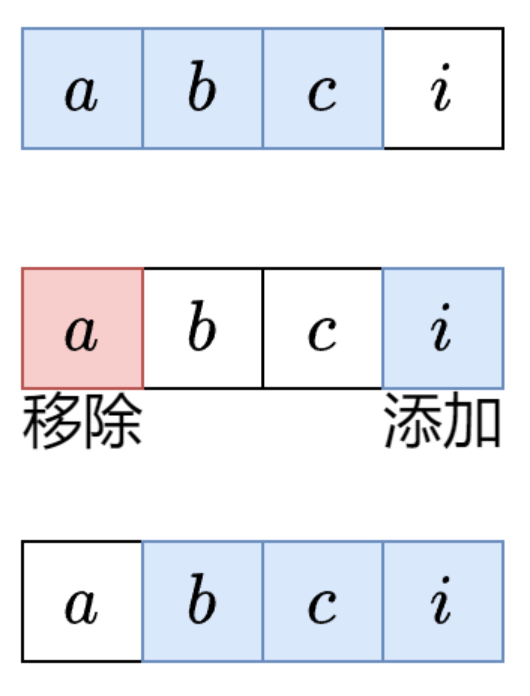

1. 入：下标为 i 的元素进入窗口，更新相关统计量。如果 i<k−1 则重复第一步。
2. 更新：更新答案。一般是更新最大值/最小值。
3. 出：下标为 i−k+1 的元素离开窗口，更新相关统计量。 以上三步适用于所有定长滑窗题目。

提示

阿囧说：代码实操中，先滑到k个窗口大小，然后位于s[i+1-k]的字符（想象指针回退k个窗口大小）先出，如果还有新字符则再次进循环，入新字符

1. 定长子串中元音的最大数目

   class Solution:
   def maxVowels(self, s: str, k: int) -> int:
       yuanYin = "aeiou"
       res = 0
       temp = 0
       for i, c in enumerate(s):
           if c in yuanYin:
               temp += 1
           if i + 1 < k:
               continue
           res = max(res, temp)
           if s[i + 1 - k] in yuanYin:
               temp -= 1
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)

2. 643. 子数组最大平均数 I

   class Solution:
   def findMaxAverage(self, nums: List[int], k: int) -> float:
       res, temp = float('-inf'), 0
       for i, num in enumerate(nums):
           temp += num
           if i + 1 < k:
               continue
           res = max(temp, res)
           temp -= nums[i + 1 - k]
       res /= k
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)

3. 1343. 大小为 K 且平均值大于等于阈值的子数组数目

   class Solution:
   def numOfSubarrays(self, arr: List[int], k: int, threshold: int) -> int:
       temp, res = 0, 0
       for i, num in enumerate(arr):
           temp += num
           if i + 1 < k:
               continue
           if temp / k >= threshold:
               res += 1
           temp -= arr[i + 1 - k]
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)

4. 2090. 半径为 k 的子数组平均值

   我的丑陋解法：

   class Solution:
   def getAverages(self, nums: List[int], k: int) -> List[int]:
       res = []
       temp, start = 0, 0
       n = len(nums)
       if n <= 2 * k:
           res = [-1] * n
           return res
       else:
           for _ in range(k):
               res.append(-1)
           for i in range(k):
               start += nums[i]
           for i, num in enumerate(nums):
               start += nums[i + k]
               if i < k:
                   continue
               res.append(start // (2 * k + 1))
               start -= nums[i - k]
               if i + k + 1 == n:
                   for _ in range(k):
                       res.append(-1)
                   break
       return res

   时间复杂度：O(n)

   空间复杂度：O(n)

   tips：但其实i应该滑到窗口的末端而不是中间，代码会简便很多

   class Solution:
   def getAverages(self, nums: List[int], k: int) -> List[int]:
       n = len(nums)
       res = [-1] * n
       temp = 0
       for i, num in enumerate(nums):
           temp += num
           if i < 2 * k:
               continue
           res[i - k] = temp // (2 * k + 1)
           temp -= nums[i - 2 * k]
       return res

   时间复杂度：O(n)

   空间复杂度：O(n)

5. 2379. 得到 K 个黑块的最少涂色次数

   class Solution:
   def minimumRecolors(self, blocks: str, k: int) -> int:
       black = 0
       res = float('inf')
       for i, c in enumerate(blocks):
           if c == 'B':
               black += 1
           if i + 1 < k:
               continue
           res = min(k - black, res)
           if blocks[i + 1 - k] == 'B':
               black -= 1
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)

6. 1052. 爱生气的书店老板

   这题有点意思

   class Solution:
   def maxSatisfied(self, customers: List[int], grumpy: List[int], minutes: int) -> int:
       cus1, cus2, temp = 0, 0, 0
       for i, (c, g) in enumerate(zip(customers, grumpy)):
           # 计算不发动技能，有多少顾客满意
           if g == 0:
               cus1 += c
           # temp记录生气导致不满意的顾客
           else:
               temp += c
           if i + 1 < minutes:
               continue
           # 用滑动窗口判断能挽回的客户最大值
           cus2 = max(cus2, temp)
           # 如果退出的窗口是生气的temp才减少
           if grumpy[i + 1 - minutes] == 1:
               temp -= customers[i + 1 - minutes]
       return cus1 + cus2

   时间复杂度：O(n)

   空间复杂度：O(1)

7. 1461. 检查一个字符串是否包含所有长度为 K 的二进制子串

   巧用集合和切片

   class Solution:
   def hasAllCodes(self, s: str, k: int) -> bool:
       set1 = set()
       temp = ''
       for i, c in enumerate(s):
           temp += c
           if i + 1 < k:
               continue
           set1.add(temp)
           temp = temp[1:]
       if len(set1) == 2 ** k:
           return True
       else:
           return False

   时间复杂度：O(nk)

   空间复杂度：O($2^k$)

8. 2841. 几乎唯一子数组的最大和

   我的使用集合写法，O(k)，总的时间复杂度是 O((n-k)*k)，不是 O(n)。当 k=n/2 时算法的时间复杂度是 O(n^2)。在力扣通过运行花了7秒，夸张QAQ。

   class Solution:
   def maxSum(self, nums: List[int], m: int, k: int) -> int:
       temp_list = []
       temp_sum = 0
       res = 0
       for i, num in enumerate(nums):
           temp_list.append(num)
           if i + 1 < k:
               continue
           if len(set(temp_list)) < m:
               temp_list = temp_list[1:]
               continue
           else:
               temp_sum = sum(temp_list)
               res = max(res, temp_sum)
           temp_list = temp_list[1:]
       return res

   时间复杂度：O(nk)

   空间复杂度：O(k)

   灵神的哈希表写法

   class Solution:
   def maxSum(self, nums: List[int], m: int, k: int) -> int:
       ans = 0
       s = sum(nums[:k - 1])  # 先统计 k-1 个数
       cnt = Counter(nums[:k - 1])
       for out, in_ in zip(nums, nums[k - 1:]):
           s += in_  # 再添加一个数就是 k 个数了
           cnt[in_] += 1
           if len(cnt) >= m:
               ans = max(ans, s)
           s -= out  # 下一个子数组不包含 out，移出窗口
           cnt[out] -= 1
           if cnt[out] == 0:
               del cnt[out]
       return ans

   时间复杂度：O(n)

   空间复杂度：O(k)

9. 2461. 长度为 K 子数组中的最大和

   我的使用集合写法，力扣超时无法通过，时代的眼泪，以后这种类型的题改为哈希表写法了。

   class Solution:
   def maximumSubarraySum(self, nums: List[int], k: int) -> int:
       temp, res = 0, 0
       for i, num in enumerate(nums):
           temp += num
           if i + 1 < k:
               continue
           if len(set(nums[i + 1 - k:i + 1])) == k:
               res = max(res, temp)
           temp -= nums[i + 1 - k]
       return res

   时间复杂度：O(nk)

   空间复杂度：O(k)

   哈希表yyds

   class Solution:
   def maximumSubarraySum(self, nums: List[int], k: int) -> int:
       temp, res = sum(nums[:k - 1]), 0
       cnt = Counter(nums[:k - 1])
       for in_, out in zip(nums[k - 1:], nums):
           # 入
           temp += in_
           cnt[in_] += 1
           # 更新
           if len(cnt) == k:
               res = max(res, temp)
           # 出
           temp -= out
           cnt[out] -= 1
           if cnt[out] == 0:
               del cnt[out]
       return res

   时间复杂度：O(n)

   空间复杂度：O(k)

10. 1423. 可获得的最大点数

    这题很有点意思

    解法一：逆向思维：求剩下的牌点数最小之和，剩下的牌一定是连续的，可以视为滑动窗口

    class Solution:
    def maxScore(self, cardPoints: List[int], k: int) -> int:
        n = len(cardPoints)
        m = n - k
        min_s = s = sum(cardPoints[:m])
        for i in range(m, n):
            s += cardPoints[i] - cardPoints[i - m]
            min_s = min(min_s, s)
        return sum(cardPoints) - min_s

    时间复杂度：O(n)

    空间复杂度：O(1)

    解法二：可以把后k个元素和前k个元素组成一个新的列表

    class Solution:
    def maxScore(self, cardPoints: List[int], k: int) -> int:
        res, temp = 0, 0
        nums = cardPoints[-k:] + cardPoints[:k]
        for i, num in enumerate(nums):
            temp += num
            if i + 1 < k:
                continue
            res = max(res, temp)
            temp -= nums[i + 1 -k]
        return res

    时间复杂度：O(k)

    空间复杂度：O(k)

    同解法二，不使用列表存储，枚举所有情况取最大值

    class Solution:
    def maxScore(self, cardPoints: List[int], k: int) -> int:
        res = temp = sum(cardPoints[:k])
        for i in range(1, k + 1):
            temp += cardPoints[-i] - cardPoints[k - i]
            res = max(res, temp)
        return res

    时间复杂度：O(k)

    空间复杂度：O(1)

11. 1652. 拆炸弹

    拆不了一点，没看懂

    class Solution:
    def decrypt(self, code: List[int], k: int) -> List[int]:
        n = len(code)
        res = [0] * n
        r = k + 1 if k > 0 else n
        k = abs(k)
        temp = sum(code[r - k:r])
        for i in range(n):
            res[i] = temp
            temp += code[(r) % n] - code[(r - k) % n]
            r += 1
        return res

    时间复杂度：O(n)

    空间复杂度：O(1)

12. 1297. 子串的最大出现次数

    汗流浃背了，使用词典的滑动窗口

    class Solution:
    def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:
        dic = defaultdict(int)
        for i in range(len(s) - minSize + 1):
            # 因为这里是字符串，所以可以通过切片快速构造滑动窗口
            temp = s[i: i + minSize]
            if len(set(temp)) <= maxLetters:
                dic[temp] += 1
        return max(dic.values()) if dic else 0

    时间复杂度：O(n * m)，其中 n 是字符串 s 的长度, m 是minSize

    空间复杂度：O(k)，其中 k 是字典中存储的不同子串的数量

    • dic = defaultdict(int)和dic = {}的区别： defaultdict(int) 会自动为新键分配默认值 0（因为 int() 的返回值是 0）。当你访问一个不存在的键时，不会引发 KeyError，而是返回 0。普通字典在访问不存在的键时，会抛出 KeyError

    • defaultdict和Counter的区别：

      • defaultdict：用于创建带有默认值的字典。可以指定默认值的类型（如 int, list, set 等）。 适用于需要管理键值对并且可能在访问时需要默认值的情况。
      • Counter：特别设计用于计数对象的出现次数。它自动将新键的计数初始化为 0，并在每次增加时更新计数。适用于频率计数和统计

    • 词典是一种基于哈希表的实现，Counter也是基于字典实现的，专注于计数

    使用Counter的滑动窗口

    class Solution:
    def maxFreq(self, s: str, maxLetters: int, minSize: int, maxSize: int) -> int:
        cnt = Counter()
        temp = ''
        for i, c in enumerate(s):
            temp += c
            if i + 1 < minSize:
                continue
            if len(set(temp)) <= maxLetters:
                cnt[temp] += 1
            temp = temp[1:]
        return max(cnt.values()) if cnt else 0

    时间复杂度：O(n * m)，其中 n 是字符串 s 的长度, m 是minSize

    空间复杂度：O(m)，其中 m 是minSize

1.2 进阶（选做）

1.3 其他（选做）

二、不定长滑动窗口

2.1 求最长/最大

提示

阿囧说：代码实操中，使用双指针left和right，right先滑到k个窗口大小，满足题目条件时停止，left开始向右移直到满足另一个条件，更新结果，再入循环

1. 无重复字符的最长子串

   class Solution:
   def lengthOfLongestSubstring(self, s: str) -> int:
       cnt = Counter()
       left = 0
       res = 0
       for right, c in enumerate(s):
           cnt[c] += 1
           while cnt[c] > 1:
               cnt[s[left]] -= 1
               left += 1
           res = max(res, right - left + 1)
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)，本题中字符均为 ASCII 字符，所以空间复杂度 ≤ O(128)

2. 3090. 每个字符最多出现两次的最长子字符串

   class Solution:
   def maximumLengthSubstring(self, s: str) -> int:
       cnt = Counter()
       left = 0
       res = 0
       for right, c in enumerate(s):
           cnt[c] += 1
           while cnt[c] > 2:
               cnt[s[left]] -= 1
               left += 1
           res = max(res, right - left + 1)
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)，本题中字符均为 ASCII 字符，所以空间复杂度 ≤ O(128)

3. 1493. 删掉一个元素以后全为 1 的最长子数组

   class Solution:
   def longestSubarray(self, nums: List[int]) -> int:
       left = 0
       cnt = Counter()
       res = 0
       for right, num in enumerate(nums):
           cnt[num] += 1
           while cnt[0] >= 2:
               cnt[nums[left]] -= 1
               left += 1
           res = max(res, right - left + 1 - cnt[0])
       return res if cnt[0] else len(nums) - 1

   时间复杂度：O(n)

   空间复杂度：O(1)，本题中字符均为 0 or 1 字符，所以空间复杂度 ≤ O(2)

4. 1208. 尽可能使字符串相等

   class Solution:
   def equalSubstring(self, s: str, t: str, maxCost: int) -> int:
       cost = []
       for c1, c2 in zip(s, t):
           cost.append(abs(ord(c1) - ord(c2)))
       left = 0
       res = 0
       sum_cost = 0
       for right, num in enumerate(cost):
           sum_cost += num
           while sum_cost > maxCost:
               sum_cost -= cost[left]
               left += 1
           res = max(res, right - left + 1)
       return res

   时间复杂度：O(n)

   空间复杂度：O(n)，cost列表的大小与输入字符串的长度相同都是 n

5. 2730. 找到最长的半重复子字符串

   class Solution:
   def longestSemiRepetitiveSubstring(self, s: str) -> int:
       left = 0
       res = 1
       same = 0
       for right in range(1, len(s)):
           if s[right] == s[right - 1]:
               same += 1
           if same == 2:
               left += 1
               while s[left] != s[left - 1]:
                   left += 1
               same = 1
           res = max(res, right - left + 1)
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)，常量辅助空间

6. 904. 水果成篮

   class Solution:
   def totalFruit(self, fruits: List[int]) -> int:
       left = 0
       res = 0
       cnt = Counter()
       for right, fruit in enumerate(fruits):
           cnt[fruit] += 1
           while len(cnt) > 2:
               cnt[fruits[left]] -= 1
               if cnt[fruits[left]] == 0:
                   del cnt[fruits[left]]
               left += 1
           res = max(res, right - left + 1)
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)，cnt只会存储 2 种水果

7. 1695. 删除子数组的最大得分

   class Solution:
   def maximumUniqueSubarray(self, nums: List[int]) -> int:
       left = 0
       res = 0
       temp = 0
       cnt = Counter()
       for right, num in enumerate(nums):
           cnt[num] += 1
           temp += num
           while cnt[num] > 1:
               cnt[nums[left]] -= 1
               temp -= nums[left]
               left += 1
           res = max(res, temp)
       return res

   时间复杂度：O(n)

   空间复杂度：O(k)， k 是 nums 中不重复元素的数量

8. 2958. 最多 K 个重复元素的最长子数组

   class Solution:
   def maxSubarrayLength(self, nums: List[int], k: int) -> int:
       left = 0
       res = 0
       cnt = Counter()
       for right, num in enumerate(nums):
           cnt[num] += 1
           while cnt[num] > k:
               cnt[nums[left]] -= 1
               left += 1
           res = max(res, right - left + 1)
       return res

   时间复杂度：O(n)

   空间复杂度：O(m)， m 是 nums 中不重复元素的数量

9. 2779. 数组的最大美丽值

   class Solution:
   def maximumBeauty(self, nums: List[int], k: int) -> int:
       left = 0
       res = 0
       nums = sorted(nums)
       for right in range(len(nums)):
           while nums[left] + k < nums[right] - k:
               left += 1
           res = max(res, right - left + 1)
       return res

   时间复杂度：O(nlogn)，其中 n 为 nums 的长度。瓶颈在排序上。虽然写了个二重循环，但是内层循环中对 left 加一的总执行次数不会超过 n 次，所以滑窗那部分的时间复杂度为 O(n)

   空间复杂度：O(1)，忽略排序的栈开销，仅用到若干额外变量

10. 2024. 考试的最大困扰度

    class Solution:
    def maxConsecutiveAnswers(self, answerKey: str, k: int) -> int:
        left = 0
        res = 0
        cnt = Counter()
        for right, c in enumerate(answerKey):
            cnt[c] += 1
            while cnt['T'] > k and cnt['F'] > k:
                cnt[answerKey[left]] -= 1
                left += 1
            res = max(res, right - left + 1)
        return res

    时间复杂度：O(n)

    空间复杂度：O(1)

11. 1004. 最大连续1的个数 III

    class Solution:
    def longestOnes(self, nums: List[int], k: int) -> int:
        left = 0
        res = 0
        from collections import Counter
        cnt = Counter()
        for right, num in enumerate(nums):
            cnt[num] += 1
            while cnt[0] > k:
                cnt[nums[left]] -= 1
                left += 1
            res = max(res, right - left + 1)
        return res

    时间复杂度：O(n)

    空间复杂度：O(1)

12. 1658. 将 x 减到 0 的最小操作数

    class Solution:
    def minOperations(self, nums: List[int], x: int) -> int:
        sum_nums = sum(nums)
        print(sum_nums)
        if sum_nums < x:
            return -1
        target = sum_nums - x
        left = 0
        temp = 0
        res = -1
        for right, num in enumerate(nums):
            temp += num
            while temp > target:
                temp -= nums[left]
                left += 1
            if temp == target:
                res = max(res, right - left + 1)
        return -1 if res < 0 else len(nums) - res

    时间复杂度：O(n)

    空间复杂度：O(1)

13. 1838. 最高频元素的频数

    class Solution:
    def maxFrequency(self, nums: List[int], k: int) -> int:
        left = 0
        temp = 0
        res = 0
        nums.sort()
        for right, num in enumerate(nums):
            temp += num
            while temp + k < num * (right - left + 1):
                temp -= nums[left]
                left += 1
            res = max(res, right - left + 1)
        return res

    时间复杂度：O(nlogn)，对 nums 数组进行排序的时间复杂度是 O(nlogn)，其中 n 是数组的长度。

    空间复杂度：O(1)

14. 2516. 每种字符至少取 K 个

    我的思路：s = "aabaaaacaabc", k = 2，cnt记录s中a、b、c出现的次数（Counter({'a': 8, 'b': 2, 'c': 2})），每一个value减去k后就是子串各字符的上限值（Counter({'a': 6, 'b': 0, 'c': 0})），目标是找到小于等于cnt的最长子串（"aaaa"），cnt2记录窗口内字符出现的次数

    class Solution:
    def takeCharacters(self, s: str, k: int) -> int:
        left = 0
        res = 0
        cnt = Counter(s)
        if cnt['a'] < k or cnt['b'] < k or cnt['c'] < k:
            return -1
        cnt2 = Counter()
        for key, value in cnt.items():
            cnt[key] -= k
        for right, c in enumerate(s):
            cnt2[c] += 1
            while cnt2['a'] > cnt['a'] or cnt2['b'] > cnt['b'] or cnt2['c'] > cnt['c']:
                cnt2[s[left]] -= 1
                left += 1
            res = max(res, right - left + 1)
        return len(s) - res

    时间复杂度：O(n)

    空间复杂度：O(1)，本题只有三种字符

    灵神的思路：与其维护窗口内的字母个数，不如直接维护窗口外的字母个数，这也是我们取走的字母个数。

    class Solution:
    def takeCharacters(self, s: str, k: int) -> int:
        cnt = Counter(s)  # 一开始，把所有字母都取走
        if any(cnt[c] < k for c in "abc"):
            return -1  # 字母个数不足 k
    
        mx = left = 0
        for right, c in enumerate(s):
            cnt[c] -= 1  # 移入窗口，相当于不取走 c
            while cnt[c] < k:  # 窗口之外的 c 不足 k
                cnt[s[left]] += 1  # 移出窗口，相当于取走 s[left]
                left += 1
            mx = max(mx, right - left + 1)
        return len(s) - mx

    时间复杂度：O(n)

    空间复杂度：O(1)，本题只有三种字符

2.2 求最短/最小

1. 209. 长度最小的子数组

   class Solution:
   def minSubArrayLen(self, target: int, nums: List[int]) -> int:
       left = 0
       res, temp = float('inf'), 0
       for right, num in enumerate(nums):
           temp += num
           while temp >= target:
               res = min(res, right - left + 1)
               temp -= nums[left]
               left += 1
       return 0 if res == float('inf') else res

   时间复杂度：O(n)

   空间复杂度：O(1)

2. 2904. 最短且字典序最小的美丽子字符串

   垃圾题目毁我青春

   class Solution:
   def shortestBeautifulSubstring(self, s: str, k: int) -> str:
       if s.count('1') < k:
           return ''
       res = s
       cnt_1 = left = 0
       for right, c in enumerate(s):
           cnt_1 += int(c)
           while cnt_1 > k or s[left] == '0':
               cnt_1 -= int(s[left])
               left += 1
           if cnt_1 == k:
               temp = s[left: right + 1]
               if (len(temp) == len(res) and temp < res) or len(temp) < len(res):
                   res = temp
       return res

   时间复杂度：O(n²)

   空间复杂度：O(n) 或 O(1)。字符串切片需要 O(n) 的空间，Go 除外。

2.3 求子数组个数

2.3.1 越长越合法

提示

一般要写 res += left。

滑动窗口的内层循环结束时，右端点固定在 right，左端点在 0,1,2,3,...,left - 1 的所有子数组（子串）都是合法的，这一共 left 个。即窗口左边的子串

1. 1358. 包含所有三种字符的子字符串数目

   class Solution:
   def numberOfSubstrings(self, s: str) -> int:
       cnt = Counter()
       left, res = 0, 0
       for i, c in enumerate(s):
           cnt[c] += 1
           while cnt['a'] > 0 and cnt['b'] > 0 and cnt['c'] > 0:
               cnt[s[left]] -= 1
               left += 1
           print(left)
           res += left
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)

2. 2962. 统计最大元素出现至少 K 次的子数组

   class Solution:
   def countSubarrays(self, nums: List[int], k: int) -> int:
       left = 0
       res = 0
       max_num_cnt = 0
       max_num = max(nums)
       for right, num in enumerate(nums):
           if num == max_num:
               max_num_cnt += 1
           while max_num_cnt == k:
               if nums[left] == max_num:
                   max_num_cnt -= 1
               left += 1
           res += left
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)

3. 3325. 字符至少出现 K 次的子字符串 I

   class Solution:
   def numberOfSubstrings(self, s: str, k: int) -> int:
       left = 0
       cnt = Counter()
       res = 0
       for right, c in enumerate(s):
           cnt[c] += 1
           while k in cnt.values():
               cnt[s[left]] -= 1
               left += 1
           res += left
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)

4. 2799. 统计完全子数组的数目

   class Solution:
   def countCompleteSubarrays(self, nums: List[int]) -> int:
       nums_class = len(set(nums))
       left = 0
       res = 0
       cnt = Counter()
       for right, num in enumerate(nums):
           cnt[num] += 1
           while len(cnt.values()) == nums_class:
               cnt[nums[left]] -= 1
               if cnt[nums[left]] == 0:
                   del cnt[nums[left]]
               left += 1
           res += left
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)

5. 2537. 统计好子数组的数目

   难点：如何记录成对元素的个数？有点数学技巧在里面，比如 nums = [1,1,1,1,1], k = 10，从第二个 1 开始，滑动窗口每增加一个 1 ，成对数量 = 当前成对数量 + 之前窗口元素个数。举例：[1,1] 是 1 对，[1,1,1] 是 1 + 2 = 3 对，[1,1,1,1] 是 3 + 3 = 6 对

   class Solution:
   def countGood(self, nums: List[int], k: int) -> int:
       left = 0
       cnt = defaultdict(int)
       res = 0
       pairs = 0
       for right, num in enumerate(nums):
           pairs += cnt[num]
           cnt[num] += 1
           while pairs >= k:
               cnt[nums[left]] -= 1
               pairs -= cnt[nums[left]]
               left += 1
           res += left
       return res

   时间复杂度：O(n)

   空间复杂度：O(n)

2.3.2 越短越合法

提示

一般要写 res += right - left + 1。

滑动窗口的内层循环结束时，右端点固定在 right，左端点在 left, left + 1, ..., right 的所有子数组（子串）都是合法的，这一共 right - left + 1 个。即窗口内的子串

1. 713. 乘积小于 K 的子数组

   class Solution:
   def numSubarrayProductLessThanK(self, nums: List[int], k: int) -> int:
       left = 0
       res = 0
       temp = 1
       if k <= 1:
           return 0
       for right, num in enumerate(nums):
           temp *= num
           while temp >= k:
               temp /= nums[left]
               left += 1
           res += right - left + 1
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)

2. 3258. 统计满足 K 约束的子字符串数量 I

   class Solution:
   def countKConstraintSubstrings(self, s: str, k: int) -> int:
       left = 0
       res = 0
       cnt = Counter()
       for right, c in enumerate(s):
           cnt[c] += 1
           while cnt['0'] > k and cnt['1'] > k:
               cnt[s[left]] -= 1
               left += 1
           res += right - left + 1
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)

3. 2302. 统计得分小于 K 的子数组数目

   class Solution:
   def countSubarrays(self, nums: List[int], k: int) -> int:
       left = 0
       res = 0
       temp = 0
       for right, num in enumerate(nums):
           temp += num
           while temp * (right - left + 1) >= k:
               temp -= nums[left]
               left += 1
           res += right - left + 1
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)

4. 2762. 不间断子数组

   我的解法：输麻了，复杂度会惩罚每一个不用模板的人

   • 时间复杂度太高了，max(temp) 和 min(temp) 都是线性时间复杂度的操作，分别需要遍历整个数组 temp 来找出最大值和最小值。因此，在最坏情况下，每次对 temp 数组的操作的时间复杂度是 O(n)，其中 n 是 temp 的长度。移除数组的第一个元素（通过 temp = temp[1:]），这也是一个 O(n) 的操作，因为每次都要更新 temp 数组。
   • 对于每个 right（即每个元素），在最坏的情况下，max(temp) 和 min(temp) 的计算需要 O(n) 时间，因此整个算法的时间复杂度是 O(n²)，其中 n 是数组的长度。

   class Solution:
   def continuousSubarrays(self, nums: List[int]) -> int:
       res = 0 
       temp = []
       for right, num in enumerate(nums):
           temp.append(num)
           while max(temp) - min(temp) > 2:
               temp = temp[1:]
           res += len(temp)
       return res

   时间复杂度：O($n^2$)

   空间复杂度：O(n)

   换上模板

   class Solution:
   def continuousSubarrays(self, nums: List[int]) -> int:
       res = 0
       left = 0
       from collections import Counter
       cnt = Counter()
       for right, num in enumerate(nums):
           cnt[num] += 1
           while max(cnt) - min(cnt) > 2:
               cnt[nums[left]] -= 1
               if cnt[nums[left]] == 0:
                           del cnt[nums[left]]
               left += 1
           res += right - left + 1
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)

2.3.3 恰好型滑动窗口

提示

例如，要计算有多少个元素和恰好等于k的子数组，可以把问题变成:

• 计算有多少个元素和 ≥ k的子数组。
• 计算有多少个元素和 > k，也就是 ≥ k+1的子数组。

答案就是元素和 ≥ k的子数组个数，减去元素和 ≥ k+1 的子数组个数。这里把>转换成≥，从而 可以把滑窗逻辑封装成一个函数 f ，然后用 f(k)-f(k + 1)计算，无需编写两份滑窗代码。

总结:「恰好」可以拆分成两个「至少」，也就是两个「越长越合法」的滑窗问题。

注:也可以把问题变成 ≤ k减去 ≤ k-1(两个至多)。可根据题目选择合适的变形方式。

注:也可以把两个滑动窗口合并起来，维护同一个右端点 right 和两个左端点 left1 和 left2，我把这种写法叫做三指针滑动窗口

1. 930. 和相同的二元子数组

   越长越合法，元素和 ≥ k的子数组个数，减去元素和 ≥ k+1 的子数组个数

   class Solution:
   def numSubarraysWithSum(self, nums: List[int], goal: int) -> int:
       def helper(k):
           left = 0
           res = 0
           temp = 0
           for right, num in enumerate(nums):
               temp += num
               while temp >= k and left <= right:
                   temp -= nums[left]
                   left += 1
               res += left
           return res
       return helper(goal) - helper(goal+1)

   时间复杂度：O(n)

   空间复杂度：O(1)

   越短越合法，元素和 ≤ k的子数组个数，减去元素和 ≤ k-1 的子数组个数

   class Solution:
   def numSubarraysWithSum(self, nums: List[int], goal: int) -> int:
       def helper(k):
           left = 0
           res = 0
           temp = 0
           for right, num in enumerate(nums):
               temp += num
               while temp > k and left <= right:
                   temp -= nums[left]
                   left += 1
               res += right - left + 1
           return res
       return helper(goal) - helper(goal-1)

   时间复杂度：O(n)

   空间复杂度：O(1)

2. 1248. 统计「优美子数组」

   越长越合法，元素和 ≥ k的子数组个数，减去元素和 ≥ k+1 的子数组个数

   class Solution:
   def numberOfSubarrays(self, nums: List[int], k: int) -> int:
       def helper(k):
           left = 0
           res = 0
           odd = 0
           for right, num in enumerate(nums):
               if num % 2 == 1:
                   odd += 1
               while odd >= k:
                   if nums[left] % 2 == 1:
                       odd -= 1
                   left += 1
               res += left
           return res
       return helper(k) - helper(k+1)

   时间复杂度：O(n)

   空间复杂度：O(1)

2.4 其他（选做）

三、单序列双指针

3.1 相向双指针

提示

阿囧说：两个指针 left= 0，right=n-1，从数组的两端开始，向中间移动，这叫相向双指针，一般用于一个数变大一个数变小。上面的滑动窗口相当于同向双指针。一般会以while开头，内部再写两个while分别控制left右移和right左移，有点像快排。注意：三个while一般都要带上 left < right，避免指针越界

1. 344. 反转字符串

   class Solution:
   def reverseString(self, s: List[str]) -> None:
       """
       Do not return anything, modify s in-place instead.
       """
       left = 0
       right = len(s) - 1
       while left < right:
           s[left], s[right] = s[right], s[left]
           left += 1
           right -= 1

   时间复杂度：O(n)

   空间复杂度：O(1)

   拓展一下，也可以使用递归来翻转字符串，不过本题要求在原地修改输入数组

   def recursion(s):
   if len(s) == 1:
       return s
   else:
       return s[-1] + recursion(s[:-1])
   
   s = "hello"
   recursion(s)

   输出：'olleh'

2. 125. 验证回文串

   class Solution:
   def isPalindrome(self, s: str) -> bool:
       s = s.lower()
       left = 0
       right = len(s) - 1
       while left < right:
           while not s[left].isalnum() and left < right:
               left += 1
           while not s[right].isalnum() and left < right:
               right -= 1
           if s[left] != s[right]:
               return False
           left += 1
           right -= 1
       return True

   时间复杂度：O(n)

   空间复杂度：O(1)

3. 1750. 删除字符串两端相同字符后的最短长度

   class Solution:
   def minimumLength(self, s: str) -> int:
       left = 0
       right = len(s) - 1
       while s[left] == s[right] and left < right:
           while s[left] == s[left+1] and left+1 < right:
               left += 1
           while s[right] == s[right-1] and left+1 < right:
               right -= 1
           left += 1
           right -= 1
       return max(0, right - left + 1)

   时间复杂度：O(n)

   空间复杂度：O(1)

4. 2105. 给植物浇水 II

   class Solution:
   def minimumRefill(self, plants: List[int], capacityA: int, capacityB: int) -> int:
       left = 0
       right = len(plants) - 1
       a, b, res = capacityA, capacityB, 0
       while left < right:
           if a < plants[left]:
               a = capacityA
               res += 1
           if b < plants[right]:
               b = capacityB
               res += 1
           a -= plants[left]
           left += 1
           b -= plants[right]
           right -= 1
       if left == right and max(a, b) < plants[left]:
               res += 1
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)

5. 977. 有序数组的平方

   相向双指针写法

   class Solution:
   def sortedSquares(self, nums: List[int]) -> List[int]:
       left = 0
       right = len(nums) - 1
       temp = right
       res = [0] * len(nums)
       while left <= right:
           if abs(nums[left]) < abs(nums[right]):
               res[temp] = nums[right] ** 2
               right -= 1
           else:
               res[temp] = nums[left] ** 2
               left += 1
           temp -= 1
       return res

   时间复杂度：O(n)

   空间复杂度：O(n)

   直接平方然后排序写法

   class Solution:
   def sortedSquares(self, nums: List[int]) -> List[int]:
       for i, num in enumerate(nums):
           nums[i] = num ** 2
       return sorted(nums)

   时间复杂度：O(nlogn)

   空间复杂度：O(n)

6. 658. 找到 K 个最接近的元素

   class Solution:
   def minimumRefill(self, plants: List[int], capacityA: int, capacityB: int) -> int:
       left = 0
       right = len(plants) - 1
       a, b, res = capacityA, capacityB, 0
       while left < right:
           if a < plants[left]:
               a = capacityA
               res += 1
           if b < plants[right]:
               b = capacityB
               res += 1
           a -= plants[left]
           left += 1
           b -= plants[right]
           right -= 1
       if left == right and max(a, b) < plants[left]:
               res += 1
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)

7. 1471. 数组中的 k 个最强值

   class Solution:
   def getStrongest(self, arr: List[int], k: int) -> List[int]:
       arr.sort()
       left = 0
       right = len(arr) - 1
       mid = (left + right) // 2
       arr[mid]
       res = []
       for i in range(k):
           if arr[right] - arr[mid] >= arr[mid] - arr[left]:
               res.append(arr[right])
               right -= 1
           else:
               res.append(arr[left])
               left += 1
       return res

   时间复杂度：O(nlogn)

   空间复杂度：O(n)

8. 167. 两数之和 II - 输入有序数组

   class Solution:
   def twoSum(self, numbers: List[int], target: int) -> List[int]:
       left = 0
       right = len(numbers) - 1
       while left < right:
           if numbers[left] + numbers[right] == target:
               return [left+1, right+1]
           elif numbers[left] + numbers[right] > target:
               right -= 1
           else:
               left += 1

   时间复杂度：O(n)

   空间复杂度：O(1)

9. 633. 平方数之和

   直接用 right = c 会超时，应该使用 right = isqrt(c)，比如 18 开根号向下取整是 4 ，那么不可能有 $5^2$ 加上一个整数的平方等于18，所以右指针只用从 4 开始向左遍历即可

   class Solution:
   def judgeSquareSum(self, c: int) -> bool:
       left = 0
       right = isqrt(c)
       while left <= right:
           if left ** 2 + right ** 2 < c:
               left += 1
           elif left ** 2 + right ** 2 > c:
               right -= 1
           else:
               return True
       return False

   时间复杂度：O($\sqrt{c}$)

   空间复杂度：O(1)

10. 2824. 统计和小于目标的下标对数目

    枚举法

    class Solution:
    def countPairs(self, nums: List[int], target: int) -> int:
        n = len(nums)
        res = 0
        for i in range(n):
            for j in range(i+1, n):
                if nums[i] + nums[j] < target:
                    res += 1
        return res

    时间复杂度：O(n^2)

    空间复杂度：O(1)

    双指针法

    class Solution:
    def countPairs(self, nums: List[int], target: int) -> int:
        res = 0
        left = 0
        right = len(nums) - 1
        nums.sort()
        while left < right:
            if nums[left] + nums[right] >= target:
                right -= 1
            else:
                res += right - left
                left += 1
        return res

    时间复杂度：O(nlogn)

    空间复杂度：O(1)

11. LCP 28. 采购方案

    class Solution:
    def purchasePlans(self, nums: List[int], target: int) -> int:
        left = 0
        right = len(nums) - 1
        res = 0
        nums.sort()
        while left < right:
            if nums[left] + nums[right] > target:
                right -= 1
            else:
                res += right - left
                left += 1
        return res%1000000007

    时间复杂度：O(nlogn)

    空间复杂度：O(1)

12. 15. 三数之和

    思路：排序复杂度为 O(nlogn)，使用三个指针 i j k ，把 i 固定住，j 和 k 相当于两数之和，i 用 for 循环复杂度为 O(n) ，j k 用相向双指针，也是 O(n) 的复杂度，故嵌套后的复杂度为 O($n^2$)，综合最后 O(nlogn) + O($n^2$) = O($n^2$)

    class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        nums.sort()
        n = len(nums)
        res = []
        for i in range(n - 2):
            if i > 0 and nums[i] == nums[i - 1]:
                continue
            j = i + 1
            k = n - 1
            while j < k:
                if nums[i] + nums[j] + nums[k] < 0:
                    j += 1
                elif nums[i] + nums[j] + nums[k] > 0:
                    k -= 1
                else:
                    res.append([nums[i], nums[j], nums[k]])
                    j += 1
                    while nums[j] == nums[j - 1] and j < k:
                        j += 1
                    k -= 1
                    while nums[k] == nums[k + 1] and j < k:
                        k -= 1
        return res

    时间复杂度：O($n^2$)

    空间复杂度：O(1)

13. 16. 最接近的三数之和

    为了判断 sum_ijk 是不是与 target 最近的数，我们还需要用一个变量 min_ 维护 ∣s−target∣ 的最小值

    class Solution:
    def threeSumClosest(self, nums: List[int], target: int) -> int:
        nums.sort()
        n = len(nums)
        min_ = float('inf')
        for i in range(n - 2):
            j = i + 1
            k = n - 1
            while j < k:
                sum_ijk = nums[i] + nums[j] + nums[k]
                if sum_ijk > target:
                    if sum_ijk - target < min_:
                        min_ = sum_ijk - target
                        res = sum_ijk
                    k -= 1
                elif sum_ijk < target:
                    if target - sum_ijk < min_:
                        min_ = target - sum_ijk
                        res = sum_ijk
                    j += 1
                else:
                    return target
        return res

    时间复杂度：O($n^2$)

    空间复杂度：O(1)

3.2 同向双指针

提示

两个指针的移动方向相同（都向右，或者都向左）。

1. 581. 最短无序连续子数组

   class Solution:
   def findUnsortedSubarray(self, nums: List[int]) -> int:
       left, right = 0, -1
       # 从左向右确定右边界
       max_num = float('-inf')
       for i in range(len(nums)):
           if nums[i] >= max_num:
               max_num = nums[i]
           else:
               right = i
       # right没变意味着非递减
       if right == -1:
           return 0
       # 从右向左确定左边界
       min_num = float('inf')
       for i in range(len(nums) - 1, -1, -1):
           if nums[i] <= min_num:
               min_num = nums[i]
           else:
               left = i
       return right - left + 1

   时间复杂度：O(n)

   空间复杂度：O(1)

3.3 背向双指针

提示

两个指针从数组中的同一个位置出发，一个向左，另一个向右，背向移动。

1. 1793. 好子数组的最大分数

   class Solution:
   def maximumScore(self, nums: List[int], k: int) -> int:
       left = right = k
       res = nums[k]
       min_num = nums[k]
       n = len(nums)
       for _ in range(n - 1):
           if right == n - 1 or left and nums[left - 1] > nums[right + 1]:
               left -= 1
               min_num = min(min_num, nums[left])
           else:
               right += 1
               min_num = min(min_num, nums[right])
           res = max(res, min_num * (right - left + 1))
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)

3.4 原地修改

1. 27. 移除元素

   class Solution:
   def removeElement(self, nums: List[int], val: int) -> int:
       k = 0
       for num in nums:
           if num != val:
               nums[k] = num
               k += 1
       return k

   时间复杂度：O(n)

   空间复杂度：O(1)

2. 26. 删除有序数组中的重复项

   class Solution:
   def removeDuplicates(self, nums: List[int]) -> int:
       k = 1
       for i in range(1, len(nums)):
           if nums[i] == nums[i - 1]:
               continue
           nums[k] = nums[i]
           k += 1
       return k

   时间复杂度：O(n)

   空间复杂度：O(1)

3. 80. 删除有序数组中的重复项 II

   需要用到双指针，有点小难

   class Solution:
   def removeDuplicates(self, nums: List[int]) -> int:
       left = 2
       for right in range(2, len(nums)):
           if nums[right] != nums[left - 2]:
               nums[left] = nums[right]
               left += 1
       return left

   时间复杂度：O(n)

   空间复杂度：O(1)

4. 283. 移动零

   class Solution:
   def moveZeroes(self, nums: List[int]) -> None:
       """
       Do not return anything, modify nums in-place instead.
       """
       left = 0
       for right in range(len(nums)):
           if nums[right] == 0:
               continue
           nums[left] = nums[right]
           left += 1
       for i in range(left, len(nums)):
           nums[i] = 0
       return nums

   时间复杂度：O(n)

   空间复杂度：O(1)

四、双序列双指针

4.1 双指针

1. 2540. 最小公共值

   class Solution:
   def getCommon(self, nums1: List[int], nums2: List[int]) -> int:
       p = q = 0
       while p < len(nums1) and q < len(nums2):
           if nums1[p] == nums2[q]:
               return nums1[p]
           elif nums1[p] < nums2[q]:
               p += 1
           else:
               q += 1
       return -1

   时间复杂度：O(n + m)，其中 n 为 nums1 的长度，m 为 nums2 的长度。

   空间复杂度：O(1)

2. 88. 合并两个有序数组

   如果我们从左往右按小的插入，会覆盖元素，因为空位在后面，因此，如果我们从右往左按大的插入，会更好操作一些

   class Solution:
   def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
       """
       Do not return anything, modify nums1 in-place instead.
       """
       i =  m - 1
       j = n - 1
       k = m + n - 1
       while j >= 0:
           if i >= 0 and nums1[i] > nums2[j]:
               nums1[k] = nums1[i]
               i -= 1
           else:
               nums1[k] = nums2[j]
               j -= 1
           k -= 1

   时间复杂度：O(n + m)，其中 n 为 nums1 的长度，m 为 nums2 的长度。

   空间复杂度：O(1)

3. 2570. 合并两个二维数组 - 求和法

   append：所见即所得，extend：迭代地添加

   my_list = [1, 2, 3]
   my_list.append([5, 6]) # 输出: [1, 2, 3, 4, [5, 6]]

   my_list = [1, 2, 3]
   my_list.extend([5, 6]) # 输出: [1, 2, 3, 4, 5, 6]

   class Solution:
   def mergeArrays(self, nums1: List[List[int]], nums2: List[List[int]]) -> List[List[int]]:
       res = []
       p = q = 0
       while 1:
           if q == len(nums2):
               res.extend(nums1[p:])
               return res
           if p == len(nums1):
               res.extend(nums2[q:])
               return res
           if nums1[p][0] == nums2[q][0]:
               res.append([nums1[p][0], nums1[p][1] + nums2[q][1]])
               p += 1
               q += 1
           elif nums1[p][0] < nums2[q][0]:
               res.append(nums1[p])
               p += 1
           else:
               res.append(nums2[q])
               q += 1

   时间复杂度：O(n + m)，其中 n 为 nums1 的长度，m 为 nums2 的长度。

   空间复杂度：O(1)

4. LCP 18. 早餐组合

   一个指针从左往右遍历第一个数组，另一个指针从右往左遍历第二个数组

   class Solution:
   def breakfastNumber(self, staple: List[int], drinks: List[int], x: int) -> int:
       res = 0
       staple.sort()
       drinks.sort()
       p = 0
       q = len(drinks) - 1
       while p < len(staple):
           if staple[p] + drinks[q] > x and q >= 0:
               q -= 1
           else:
               res = res + q + 1
               p += 1
       return res % 1000000007

   时间复杂度：O(nlogn + mlogm + n + m) = O(nlogn + mlogm)，其中 n 为 staple 的长度，m 为 drinks 的长度。

   空间复杂度：O(1)

5. 1385. 两个数组间的距离值

   枚举法

   class Solution:
   def findTheDistanceValue(self, arr1: List[int], arr2: List[int], d: int) -> int:
       res = 0
       for i in range(len(arr1)):
           for j in range(len(arr2)):
               if abs(arr1[i] - arr2[j]) <= d:
                   res -= 1
                   break
           res += 1
       return res

   时间复杂度：O(n * m)

   空间复杂度：O(1)

   双指针法

   class Solution:
   def findTheDistanceValue(self, arr1: List[int], arr2: List[int], d: int) -> int:
       arr1.sort()
       arr2.sort()
       left ,right, res = 0, 0, 0
       for num in arr1:
           while left < len(arr2) and arr2[left] + d < num:
               left += 1
           while right < len(arr2) and arr2[right] - d <= num:
               right += 1
           if left == right:
               res += 1
       return res

   时间复杂度：O(nlogn)

   空间复杂度：O(1)

6. 1855. 下标对中的最大距离

   class Solution:
   def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:
       res = 0
       j = 0
       for i in range(len(nums1)):
           while j < len(nums2) and nums1[i] <= nums2[j]:
               j += 1
           res = max(res, j - i - 1)
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)

7. 925. 长按键入

   class Solution:
   def isLongPressedName(self, name: str, typed: str) -> bool:
       i = 0
       j = 0
       while j < len(typed):
           if i <len(name) and name[i] == typed[j]:
               i += 1
               j += 1
           elif j > 0 and name[i - 1] == typed[j]:
               j += 1
           else:
               return False
       return i == len(name)

   时间复杂度：O(n)

   空间复杂度：O(1)

4.2 判断子序列

提示

阿囧说：外层遍历长串，好的情况可以是没遍历完就找到了，最坏情况遍历完才知道不符合

1. 392. 判断子序列

   class Solution:
   def isSubsequence(self, s: str, t: str) -> bool:
       if s == "":
           return True
       i = 0
       for j in range(len(t)):
           if s[i] == t[j]:
               i += 1
               if i == len(s):
                   return True
       return False

   时间复杂度：O(m)，其中 m 是 t 的长度。代码只有一个循环，至多循环 O(m) 次。

   空间复杂度：O(1)

2. 524. 通过删除字母匹配到字典里最长单词

   class Solution:
   def findLongestWord(self, s: str, dictionary: List[str]) -> str:
       res = ""
       for dic in dictionary:
           dic_left = 0
           for c in s:
               if c == dic[dic_left]:
                   dic_left += 1
                   if dic_left == len(dic):
                       if len(dic) > len(res) or (len(dic) == len(res) and dic < res):
                           res = dic
                       break
       return res

   时间复杂度：O(n * m)

   空间复杂度：O(1)

3. 2486. 追加字符以获得子序列

   class Solution:
   def appendCharacters(self, s: str, t: str) -> int:
       t_left = 0
       for s_c in s:
           if s_c == t[t_left]:
               t_left += 1
               if t_left == len(t):
                   return 0
       return len(t) - t_left

   时间复杂度：O(n)

   空间复杂度：O(1)

4. 2825. 循环增长使字符串子序列等于另一个字符串

   class Solution:
   def canMakeSubsequence(self, str1: str, str2: str) -> bool:
       str2_left = 0
       for c in str1:
           if c == str2[str2_left] or (ord(str2[str2_left]) - ord(c) + 26) % 26 == 1:
               str2_left += 1
               if str2_left == len(str2):
                   return True
       return False

   时间复杂度：O(n)

   空间复杂度：O(1)

五、三指针

注：部分题目已整理到「2.3.3 恰好型滑动窗口」中。

1. 2367. 等差三元组的数目

   class Solution:
   def arithmeticTriplets(self, nums: List[int], diff: int) -> int:
       res = 0
       for i in range(len(nums)):
           if nums[i] + diff in nums and nums[i] + 2 * diff in nums:
               res += 1
       return res

   时间复杂度：O(n)

   空间复杂度：O(1)

2. 2563. 统计公平数对的数目

   两个指针left和right从后往前找到符合的区间，计算区间元素个数，第三个指针从前往后遍历。

   class Solution:
   def countFairPairs(self, nums: List[int], lower: int, upper: int) -> int:
       nums.sort()
       res = 0
       left = right = len(nums)
       for j, num in enumerate(nums):
           while right and nums[right - 1] > upper - num:
               right -= 1
           while left and nums[left - 1] >= lower - num:
               left -= 1
           res += min(j, right) - min(j, left)
       return res

   时间复杂度：O(nlogn)

   空间复杂度：O(1)

思考

做了一些题目后，请总结：滑动窗口和双指针的区别是什么？

提示

阿囧说：滑动窗口需要维护窗口内的状态，整个窗口内的元素共同构成了正确答案；
双指针更多的是考虑两个具体指针处的状态，指针中间则不考虑，同向双指针和滑动窗口最为接近。