一、二分查找

暴力做法：遍历每个数，询问他是否 ≥ target？

时间复杂度：O(n)

二分做法：

要求 nums 是非递减的，即 nums[i] <= nums[i + 1]

返回第一个大于等于 target 的 i，如果不存在，返回 len(nums)

如果 target 在 M 右边，那么将 L 更新到 M + 1

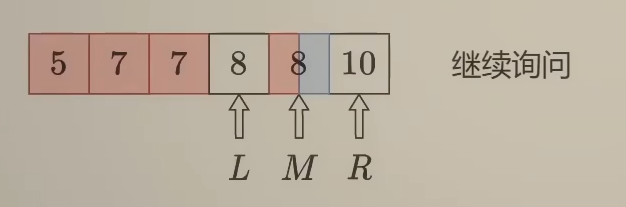
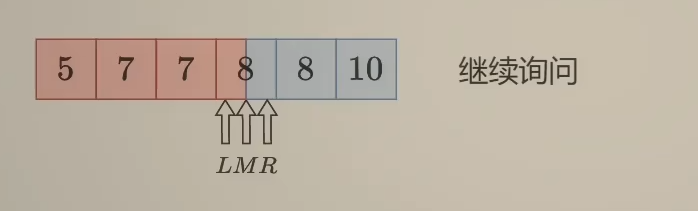
其他语言直接相加可能会溢出，可改为 mid = left + (right - left) // 2

# 左右闭区间写法
def b_s(nums, target):
    left = 0
    right = len(nums) - 1 # 区间 [left, right]
    while left <= right:
        mid = (left + right) // 2
        if nums[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return left # right + 1

# 左闭右开区间写法
def b_s2(nums, target):
    left = 0
    right = len(nums) # 区间 [left, right)
    while left < right:
        mid = (left + right) // 2
        if nums[mid] < target:
            left = mid + 1
        else:
            right = mid
    return left # right

# 左右开区间写法
def b_s3(nums, target):
    left = -1
    right = len(nums) # 区间 (left, right)
    while left + 1 < right:
        mid = (left + right) // 2
        if nums[mid] < target:
            left = mid
        else:
            right = mid
    return left + 1 # right

nums = [5,7,7,8,8,10], target = 8

上面是 ≥ target 写法，记为 ≥ x

如果是 > target，可以转换为 ≥ x + 1，使用 b_s(nums, target + 1)

如果是 < target，可以转换为 (≥ x) - 1，使用 b_s(nums, target) - 1

如果是 ≤ target，可以转换为 (> x) - 1，使用 b_s(nums, target + 1) - 1

时间复杂度：O(logn)

空间复杂度：O(1)

1. 34. 在排序数组中查找元素的第一个和最后一个位置

   class Solution:
   def searchRange(self, nums: List[int], target: int) -> List[int]:
       def b_s(nums, target):
           left = 0
           right = len(nums) - 1
           while left <= right:
               mid = (left + right) // 2
               if nums[mid] < target:
                   left = mid + 1
               else:
                   right = mid - 1
           return left
   
       start = b_s(nums, target)
       end = b_s(nums, target + 1) - 1
       if len(nums) == 0 or start > end:
           return [-1, -1]
       return [start, end]

   时间复杂度：O(logn)

   空间复杂度：O(1)

2. 35. 搜索插入位置

   class Solution:
   def searchInsert(self, nums: List[int], target: int) -> int:
       left = 0
       right = len(nums) - 1
       while left <= right:
           mid = (left + right) // 2
           if nums[mid] < target:
               left = mid + 1
           else:
               right = mid - 1
       return left

   时间复杂度：O(logn)

   空间复杂度：O(1)

3. 704. 二分查找

   class Solution:
   def search(self, nums: List[int], target: int) -> int:
       left = 0
       right = len(nums) - 1
       while left <= right:
           mid = (left + right) // 2
           if nums[mid] < target:
               left = mid + 1
           else:
               right = mid - 1
       return -1 if left == len(nums) or nums[left] != target else left

   时间复杂度：O(logn)

   空间复杂度：O(1)

4. 744. 寻找比目标字母大的最小字母

   class Solution:
   def nextGreatestLetter(self, letters: List[str], target: str) -> str:
       target = chr(ord(target) + 1)
       left = 0
       right = len(letters) - 1
       while left <= right:
           mid = (left + right) // 2
           if letters[mid] < target:
               left = mid + 1
           else:
               right = mid - 1
       return letters[0] if left == len(letters) else letters[left]

   时间复杂度：O(logn)

   空间复杂度：O(1)

5. 2529. 正整数和负整数的最大计数

   class Solution:
   def maximumCount(self, nums: List[int]) -> int:
       def b_s(nums, target):
           left = 0
           right = len(nums) - 1
           while left <= right:
               mid = (left + right) // 2
               if nums[mid] < target:
                   left = mid + 1
               else:
                   right = mid - 1
           return left
   
       neg = b_s(nums, 0)
       pos = len(nums) - b_s(nums, 1)
       return max(neg, pos)

   时间复杂度：O(logn)

   空间复杂度：O(1)

   才知道可以 from bisect import bisect_left ，直接调用 bisect_left 求第一个 ≥ target， bisect_right 求第一个 > target 的，一直都是手搓二分┭┮﹏┭┮

   class Solution:
   def maximumCount(self, nums: List[int]) -> int:
       neg = bisect_left(nums, 0)
       pos = len(nums) - bisect_right(nums, 0)
       return max(neg, pos)

   时间复杂度：O(logn)

   空间复杂度：O(1)

6. 1385. 两个数组间的距离值

   class Solution:
   def findTheDistanceValue(self, arr1: List[int], arr2: List[int], d: int) -> int:
       arr2.sort()
       res = 0
       for x in arr1:
           left = bisect_left(arr2, x - d)
           right = bisect_left(arr2, x + d)
           if left == right:
               if left < len(arr2):
                   if arr2[left] != x + d and arr2[left] != x - d:
                       res += 1
               else:
                   res += 1
       return res

   时间复杂度：O(nlogn)

   空间复杂度：O(1)

7. 2300. 咒语和药水的成功对数

   class Solution:
   def successfulPairs(self, spells: List[int], potions: List[int], success: int) -> List[int]:
       potions.sort()
       res = []
       for sp in spells:
           if success // sp == success / sp:
               res.append(len(potions) - bisect_left(potions, success // sp))
           else:
               res.append(len(potions) - bisect_right(potions, success // sp))
       return res

   时间复杂度：O((n+m)logm)，其中 n 为 spells 的长度，m 为 potions 的长度。排序 O(mlogm)。二分 n 次，每次 O(logm)。

   空间复杂度：O(n)

8. 2389. 和有限的最长子序列

   class Solution:
   def answerQueries(self, nums: List[int], queries: List[int]) -> List[int]:
       nums.sort()
       res = []
       for q in queries:
           left = 0
           right = len(nums) - 1
           while left <= right:
               mid = (left + right) // 2
               if sum(nums[:mid + 1]) <= q:
                   left = mid + 1
               else:
                   right = mid - 1
           res.append(left)
       return res

   时间复杂度：O((n+m)logn)，其中 n 为 nums 的长度，m 为 queries 的长度。排序为 O(nlogn)，m 次二分查找为 O(mlogn)。

   空间复杂度：O(n)

   灵神用了一个前缀和，可以直接使用 bisect ，简单了非常多！你是我的神！

   class Solution:
   def answerQueries(self, nums: List[int], queries: List[int]) -> List[int]:
       nums.sort()
       res = []
       for i in range(1, len(nums)):
           nums[i] += nums[i - 1]
       for x in queries:
           res.append(bisect_right(nums, x))
       return res

   时间复杂度：O((n+m)logn)，其中 n 为 nums 的长度，m 为 queries 的长度。排序为 O(nlogn)，m 次二分查找为 O(mlogn)。

   空间复杂度：O(n)

9. 1170. 比较字符串最小字母出现频次

   纯模拟，感觉写复杂了，倒是能过

   class Solution:
   def numSmallerByFrequency(self, queries: List[str], words: List[str]) -> List[int]:
   
       def f(s):
           min_c = 'z'
           cnt = 0
           for c in s:
               if c < min_c:
                   min_c = c
                   cnt = 1
               elif c == min_c:
                   cnt += 1
           return cnt
   
       for i, w in enumerate(words): # m
           words[i] = f(w) # L_avg
       words.sort() # mlogm
       res = []
       for q in queries: # n
           target = f(q) # L_avg
           res.append(len(words) - bisect_right(words, target)) # logm
       return res

   时间复杂度：O(m * L_avg + m log m + n * (L_q + log m))，m 是单词列表 words 的大小。n 是查询列表 queries 的大小。L_avg 是单词的平均长度。L_q 是查询的平均长度。

   空间复杂度：O(n)

二、二分答案

2.1 求最小

提示

阿囧说：如果答案有单调性，那么可以二分答案。这种类型的题，要找好二分的左右端点，左右端点一般是可以继续优化的，从而降低时间复杂度

1. 1283. 使结果不超过阈值的最小除数

   我最初的写法过了 70/71 个样例，最后一个过不了，太抽象了

   class Solution:
   def smallestDivisor(self, nums: List[int], threshold: int) -> int:
   
       def division_up(x, l):
           if x // l == x / l:
               return x // l
           else:
               return x // l + 1
   
       left = 0
       right = max(nums)
       while left + 1 < right:
           mid = (left + right) // 2
           if sum(division_up(num, mid) for num in nums) <= threshold:
               right = mid
           else:
               left = mid
       return right

   时间复杂度：O(nlogU)，其中 n 是 nums 的长度，U=max(nums)。二分 O(logU) 次，每次 O(n) 遍历 nums。

   空间复杂度：O(1)

2. 2187. 完成旅途的最少时间

   class Solution:
   def minimumTime(self, time: List[int], totalTrips: int) -> int:
       left = 0
       right = min(time) * totalTrips
       while left + 1 < right:
           mid = (left + right) // 2
           if sum(mid // t for t in time) < totalTrips:
               left = mid
           else:
               right = mid
       return right

   时间复杂度：O(nlogU)，其中 n 为 time 的长度，U 为二分上下界之差。在本题数据范围下，U 不会超过 $10^{14}$

   空间复杂度：O(1)

3. 1870. 准时到达的列车最小时速

   class Solution:
   def minSpeedOnTime(self, dist: List[int], hour: float) -> int:
       if len(dist) >= hour + 1:
           return -1
   
       def division_up(x, l):
           if x // l == x / l:
               return x // l
           else:
               return x // l + 1
   
       left = 0
       right = max(dist) * 100
       while left + 1 < right:
           mid = (left + right) // 2
           if sum(division_up(d, mid) for d in dist[:-1]) + dist[-1] / mid <= hour:
               right = mid
           else:
               left = mid
       return right

   时间复杂度：O(nlogU)，其中 n 是 dist 的长度，U 为二分上下界之差。在本题数据范围下，U 不会超过 $10^7$

   空间复杂度：O(1)

4. 1011. 在 D 天内送达包裹的能力

   很明显，这种题型的 check 函数很好写，只要不断优化 left 和 right 就能过了

   class Solution:
   def shipWithinDays(self, weights: List[int], days: int) -> int:
   
       def check(weights, min_weights):
           now = 0
           res = 0
           for w in weights:
               now += w
               if now < min_weights:
                   continue
               res += 1
               now = w
           return res
   
       left = max(weights)
       right = sum(weights) + 1
       while left + 1 < right:
           mid = (left + right) // 2
           if check(weights, mid) < days:
               right = mid
           else:
               left = mid
       return left

   时间复杂度：O(nlogU)，其中 n 是 weights 的长度，U 为二分上下界之差。

   空间复杂度：O(1)

5. 875. 爱吃香蕉的珂珂

   class Solution:
   def minEatingSpeed(self, piles: List[int], h: int) -> int:
   
       def division_up(x, l):
           if x // l == x / l:
               return x // l
           else:
               return x // l + 1
   
       left = 0
       right = max(piles)
       while left + 1 < right:
           mid = (left + right) // 2
           if sum(division_up(p, mid) for p in piles) <= h:
               right = mid
           else:
               left = mid
       return right

   时间复杂度：O(nlogU)，其中 n 是 piles 的长度，U 为 max(piles)。

   空间复杂度：O(1)

2.2 求最大

提示

灵神：在练习时，请注意「求最小」和「求最大」的二分写法上的区别。

前面的「求最小」和二分查找求「排序数组中某元素的第一个位置」是类似的，按照红蓝染色法，左边是不满足要求的（红色），右边则是满足要求的（蓝色）。

「求最大」的题目则相反，左边是满足要求的（蓝色），右边是不满足要求的（红色）。这会导致二分写法和上面的「求最小」有一些区别。

以开区间二分为例：

• 求最小：check(mid) == true 时更新 right = mid，反之更新 left = mid，最后返回 right。
• 求最大：check(mid) == true 时更新 left = mid，反之更新 right = mid，最后返回 left。

对于开区间写法，简单来说 check(mid) == true 时更新的是谁，最后就返回谁。相比其他二分写法，开区间写法不需要思考加一减一等细节，个人推荐使用开区间写二分。

sas sas

1. 275. H 指数 II

   最初的想法没有利用 citations 已经是有序的性质，check函数的时间复杂度是O(n)，导致最终是O(nlogn)，居然也能过

   class Solution:
   def hIndex(self, citations: List[int]) -> int:
   
       def check(citations, mid):
           res = 0
           for c in citations:
               if c >= mid:
                   res += 1
           return True if res >= mid else False
   
       left = -1
       right = len(citations) + 1
       while left + 1 < right:
           mid = (left + right) // 2
           if check(citations, mid):
               left = mid
           else:
               right = mid    
       return left

   时间复杂度：O(nlogn)，其中 n 是 citations 的长度。

   空间复杂度：O(1)

   利用 citations 有序

   class Solution:
   def hIndex(self, citations: List[int]) -> int:
       left = -1
       right = len(citations) + 1
       while left + 1 < right:
           mid = (left + right) // 2
           if citations[-mid] >= mid:
               left = mid
           else:
               right = mid    
       return left

   时间复杂度：O(logn)，其中 n 是 citations 的长度。

   空间复杂度：O(1)

2. 2226. 每个小孩最多能分到多少糖果

   class Solution:
   def maximumCandies(self, candies: List[int], k: int) -> int:
       left = 0
       right = max(candies) + 1
       while left + 1 < right:
           mid = (left + right) // 2
           if sum(c // mid for c in candies) < k:
               right = mid
           else:
               left = mid
       return left

   时间复杂度：O(nlogU)，其中 n 是 candies 的长度，U 为 max(candies) + 1。

   空间复杂度：O(1)

三、二分间接值

提示

二分的不是答案，而是一个和答案有关的值（间接值）。

1. 3143. 正方形中的最多点数

   我是究极无敌模拟怪

   class Solution:
   def maxPointsInsideSquare(self, points: List[List[int]], s: str) -> int:
       # 二分正方形的边长，先定义二分的左右边界
       left = -1
       new_points = []
       for p in points: # 将二维列表转化为一维列表
           new_points.append(max(abs(p[0]), abs(p[1])))
       right = max(new_points) + 1
   
       # 符合题意的 check 函数：超过两个相同的字母返回 False
       def check(new_points, mid):
           cnt = Counter()
           for i, n in enumerate(new_points):
               if n <= mid:
                   cnt[s[i]] += 1
                   if cnt[s[i]] == 2:
                       return False
           return True
   
       # 二分得到符合 check 的最大边长
       while left + 1 < right:
           mid = (left + right) // 2
           if check(new_points, mid):
               left = mid
           else:
               right = mid
   
       # 通过最大边长计算包含的点数 res
       res = 0
       for n in new_points:
           if n <= left:
               res += 1
       return res

   时间复杂度：O(nlogU)，其中 n 是 points 的长度，U 为 max(points)。

   空间复杂度：O(n)

四、最小化最大值

本质是二分答案求最小。二分的 mid 表示上界。

1. 410. 分割数组的最大值

   class Solution:
   def splitArray(self, nums: List[int], k: int) -> int:
   
       # 根据当前子数组最大值，返回子数组的个数
       def check(nums, mid):
           temp = 0
           res = 1
           for num in nums:
               temp += num
               if temp <= mid:
                   continue
               res += 1
               temp = num
           return res
   
       left = max(nums) - 1 # k = len(nums)
       right = sum(nums) + 1 # k = 1
       while left + 1 < right:
           mid = (left + right) // 2
           if check(nums, mid) <= k: # k变大输出会变小，因此 check 小于 k 时，想让 k 变大 mid 要变小
               right = mid
           else:
               left = mid
       return right

   时间复杂度：O(nlogU)，其中 n 是 candies 的长度，U 为 sum(nums) - max(nums)。

   空间复杂度：O(1)

2. 2064. 分配给商店的最多商品的最小值

   class Solution:
   def minimizedMaximum(self, n: int, quantities: List[int]) -> int:
   
       def divide_up(x, l):
           if x // l == x / l:
               return x // l
           else:
               return x // l + 1
   
       left = 0
       right = max(quantities)
       while left + 1 < right:
           mid = (left + right) // 2
           if sum(divide_up(q, mid) for q in quantities) <= n:
               right = mid
           else:
               left = mid
       return right

   时间复杂度：O(nlogU)，其中 n 是 quantities 的长度，U 为 max(quantities)。

   空间复杂度：O(1)

3. 1760. 袋子里最少数目的球

   主打一个代码又臭又长，没有技巧，全是模拟

   class Solution:
   def minimumSize(self, nums: List[int], maxOperations: int) -> int:
   
       def help(x, l):
           """
           返回x分成一个个不超过l的数需要的次数
           >>>help(9, 2)
           >>>4
           >>>help(8, 2)
           >>>3
           """
           if x // l == x / l:
               return x // l - 1
           else:
               return x // l
   
       def check(nums, mid):
           res = 0
           for num in nums:
               if num > mid:
                   res += help(num, mid)
                   if res > maxOperations:
                       return False
           return True
   
       left = 0
       right = max(nums)
       while left + 1 < right:
           mid = (left + right) // 2
           if check(nums, mid):
               right = mid
           else:
               left = mid
       return right

   时间复杂度：O(nlogU)，其中 n 是 nums 的长度，U 为 max(nums)。

   空间复杂度：O(1)