1. 84. 柱状图中最大的矩形

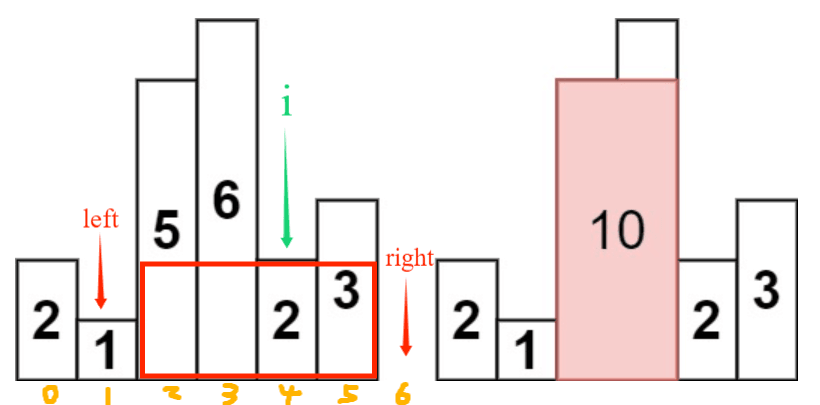
   用 i 遍历每一根柱子，提前计算出当前柱子（举例：下标4）的左右可扩容区间。

   方法：找出左边第一个比当前柱子矮的柱子（下标1），矮柱（下标1）和当前柱子之间的就是可扩容的（下标2和3可作为下标4的左边扩容），右边同理。

   class Solution:
   def largestRectangleArea(self, heights: List[int]) -> int:
       n = len(heights)
       st = []
       left = [-1] * n
       right = [n] * n
       for i, h in enumerate(heights):
           while st and heights[st[-1]] >= h:
               j = st.pop()
               right[j] = i
           if st:
               left[i] = st[-1]
           st.append(i)
   
       res = 0
       for i, h in enumerate(heights):
           res = max(res, h * (right[i] - left[i] - 1))
       return res

   时间复杂度：O(n)，其中 n 为 heights 的长度。

   空间复杂度：O(n)

2. 1793. 好子数组的最大分数

   遍历每一个元素，计算出每一个元素左边和右边第一个比他小的，作为左右开区间，这个区间就是这个元素的好子数组的最大分数，注意最后要加一个 if 判断：一个好子数组的两个端点下标需要满足 i <= k <= j

   class Solution:
   def maximumScore(self, nums: List[int], k: int) -> int:
       n = len(nums)
       st = []
       left = [-1] * n
       right = [n] * n
       for i, num in enumerate(nums):
           while st and nums[st[-1]] >= num:
               j = st.pop()
               right[j] = i
           if st:
               left[i] = st[-1]
           st.append(i)
       res = 0
       for i, num in enumerate(nums):
           if left[i] < k and right[i] > k:
               res = max(res, num * (right[i] - left[i] - 1))
       return res

   时间复杂度：O(n)，其中 n 为 nums 的长度。

   空间复杂度：O(n)